FPの勉強を始めたときに割と最初に資産形成に使用する6つの係数が紹介されています。
テキストでは係数は問題で与えられるから名前だけ覚える感じで式などの説明がなく、
あまりピンときませんでした。
そこで、自分で計算してイメージしながら覚えました。
6つの係数は以下になります。
・終価係数
・現価係数
・年金終価係数
・年金現価係数
・資本回収係数
・減債基金係数
4年の運用を例に1つ1つ説明していきます。
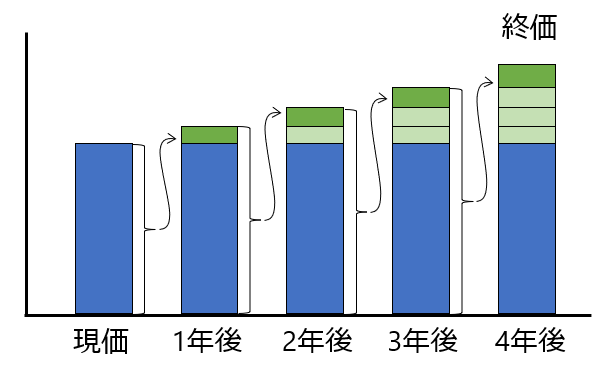
計算式の前にグラフで説明すると下のようになります。
前年の利息分も含めて利息を計算するので複利になります。
終価係数は複利が積みあがったものを計算し、現価係数は希望の終価を得るための
現価を計算します。
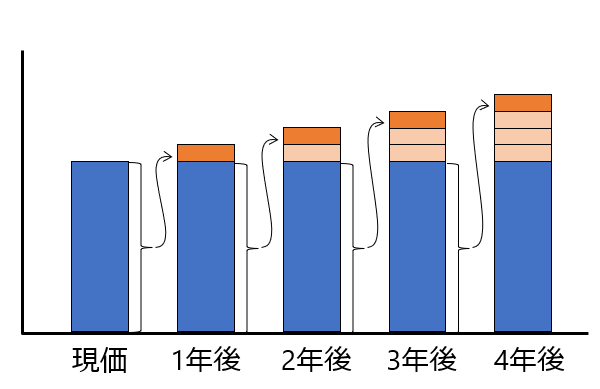
ちなみに、単利は下のようになり、利息だけを比較するとこんな感じです。
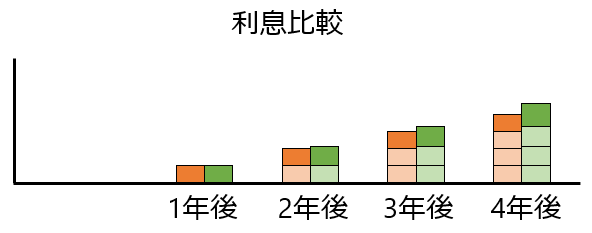
じわじわと差が広がっていくのがわかります。
まず、終価係数と現価係数の計算式は以下になります。
・終価係数
複利で資本の現価(既知)を運用した時の係数
$$現価\times(1+年利)×(1+年利)×(1+年利)\times(1+年利)=終価$$
$$現価×(1+年利)^4=終価$$
・現価係数
複利で5年間運用したときに目標の終価(既知)を得るための現価を求める係数
終価係数を整理することで求めます。
$$現価×(1+年利)^4=終価$$
$$終価×\frac{1}{(1+年利)^4}=現価$$
次に積立ながら運用した時のグラフは下のようになります。
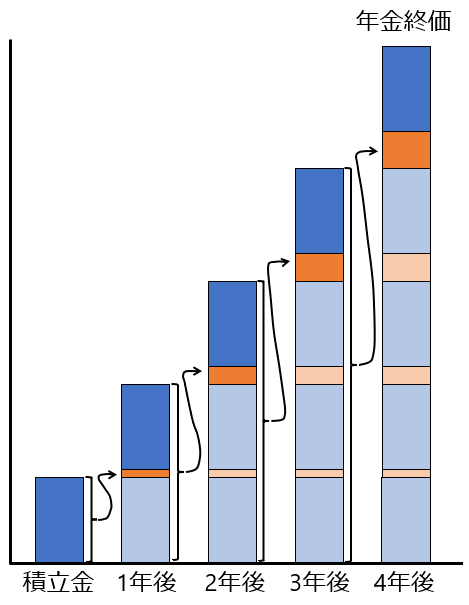
利息がだんだんと大きくなっていくのがわかります。
想定年数の積立てた年金終価を計算するのが年金終価係数、
積立金額を計算するのが減債基金係数になります。
・年金終価係数
3年間積立金(既知)を積立ながら運用をした時に得られる年金終価を求める係数
$$[\{積立金 \times (1 + 年利) + 積立金\} \times (1 + 年利) + 積立金]\times(1 + 年利) + 積立金= 年金終価$$
この式を展開して整理すると
$$積立金 \times \{(1 + 年利)^3 +(1 + 年利)^2 + (1 + 年利) + 1\} = 年金終価$$
$$積立金 \times \sum_{i=1}^{4} (1 + 年利)^{4-i} = 年金終価$$
・減債基金係数
3年間積立ながら運用したときに得たい年金終価(既知)を形成するための積立金を求める係数
先ほどの年金終価係数を整理することで求めます。
$$積立金 \times \sum_{i=1}^{4} (1 + 年利)^{4-i} = 年金終価$$
$$年金終価 \times \frac{1}{ \sum_{i=1}^{4} (1 + 年利)^{4-i} } = 積立金$$
次に取り崩しながら運用するときのグラフを下に示します。
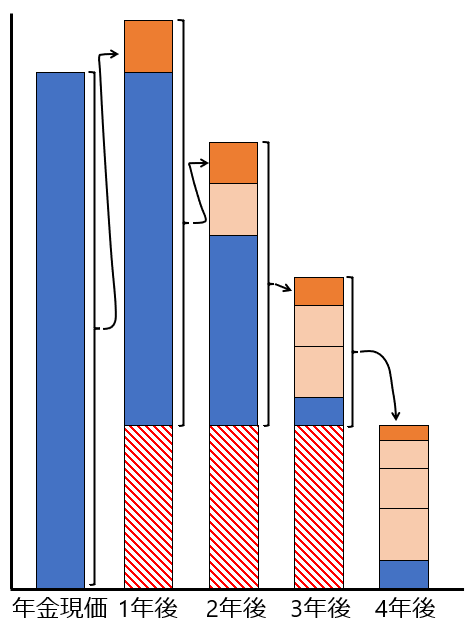
先ほどの年金終価係数で積みあがった年金を何年で取り崩すか、
みたいな計算ができるようになります。
元の金額が大きいので利息も大きくなり、最後の年はほとんど利息で補えています。
では、計算式を下に示していきます。
・資本回収係数
3年間年金現価(既知)を運用しながら一定金額の回収金を回収し、4年間で回収しきる金額を求める係数
$$(((年金現価 \times (1 + 年利) – 回収金) \times (1 + 年利) – 回収金) \times (1 + 年利) – 回収金 ) \times (1 + 年利) – 回収金= 0$$
この式を展開して整理すると
$$年金現価 \times (1 + 年利)^4 – 回収金 \times \{(1 + 年利)^3 + (1 + 年利)^2 + (1 + 年利)^1 + 1\} = 0$$
$$年金現価 \times \frac{(1 + 年利)^4}{\{(1 + 年利)^3 + (1 + 年利)^2 + (1 + 年利)^1 + 1\}} = 回収金$$
$$年金現価 \times \frac{(1 + 年利)^4}{\sum_{i=1}^{4} (1 + 年利)^{4-i}} = 回収金$$
・年金現価係数
3年間で一定金額の回収金(既知)で年金現価を回収しきるときの年金現価を求める係数
先ほどの資本回収係数を整理することで求めます。
$$年金現価 \times \frac{(1 + 年利)^4}{\sum_{i=1}^{4} (1 + 年利)^{4-i}} = 回収金$$
$$回収金 \times \frac{\sum_{i=1}^{4}{ (1 + 年利)^{4-i}}}{(1 + 年利)^4} = 年金現価$$
この式を使えばざっくりで資産の計算ができるようになります。


